Bounding Regions

Bounding region information for a symbol, or groups of symbols, is important as it is used in the building of arcs between nodes, as described in Section 3.1.4, and deciding whether or not to apply rules, as described later in Section 3.1.6.

  

Figure 3.2: Construction of bounding regions.

(a) Rectangular Regions.

(b) Individual Rectangular Regions.

(c) Smallest Convex Hull.

 

Figure 3.2 shows three different methods for managing bounding regions. Figure 3.2(a) is the approach used by this system. The original bounding boxes are the smallest rectangles that enclose the symbols' strokes. When combined, the new bounding box is made from the outermost extents of the bounding boxes of the original symbols. Other approaches are to keep track of the individual bounding boxes that went into it, as shown in Figure 3.2(b), though this raises the issue of how to deal with the gaps between the boxes. Figure 3.2(c) illustrates the use of the smallest convex hull around the pixels or strokes of the original characters, as Miller and Viola do . When the symbols are combined, the new bounding region is the smallest convex hull enclosing all the symbols.

  

Figure 3.3: These bounding boxes overlap, although the symbols do not.

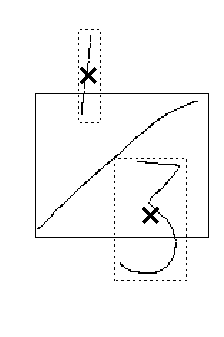
The only disadvantage of using rectangular bounding boxes is that the bounding box of sloped characters is excessively large and takes in a large amount of empty space. As a result, users can accidentally put things overlapping or inside other symbols without intending to. Figure  demonstrates this. From the user's point of view, the characters do not overlap, but a system which works with the bounding boxes will say they do. This causes problems when parsing the formula, as the system will interpret the geometric relationship between the symbols incorrectly. As a result, the formula will either be misparsed or be completely unparsable.

  

Figure 3.4: Using centre points instead of bounding boxes for geometric tests. While the 1 is outside the fraction bar's bounding box, the 3 is not.

Treating the symbol you are testing against another as a central point, and seeing if this point is inside the other's bounding box helps, but the problem can still occur. Figure 3.4 shows that the centre point of the 1 is not inside the fraction bar, but the centre point of the 3 still is. The use of this approach has, in spite of this problem, worked well unless users write excessively sloped fraction bars or integral symbols.

It is in situations like this that Miller and Viola's  convex hull approach for bounding regions is much better. The computational complexity for creating complex hulls from a set of n pixels is $O(n \log n)$. The union of two convex hulls can be computed in O(l + m), where l and m are the number of vertices in the convex hulls. The intersection of two convex hulls can be determined in O(l + m) also. Convex hulls will also at times take in large amounts of empty space for large subexpressions in a formula, as the rectangular regions do, but for single symbols the area they cover is more intuitively what ``belongs'' to a single symbol. In the case of a sloped fraction bar, a problem for rectangular bounding regions, the convex hull approach is a great improvement.

This system does not use the convex hull approach due to the fact that it was discovered after the system was already using rectangular regions. The rectangular regions work well enough that changing the system to use convex hulls is not currently necessary.

convex hull approach for bounding regions is much better. The computational complexity for creating complex hulls from a set of n pixels is $O(n \log n)$. The union of two convex hulls can be computed in O(l + m), where l and m are the number of vertices in the convex hulls. The intersection of two convex hulls can be determined in O(l + m) also. Convex hulls will also at times take in large amounts of empty space for large subexpressions in a formula, as the rectangular regions do, but for single symbols the area they cover is more intuitively what ``belongs'' to a single symbol. In the case of a sloped fraction bar, a problem for rectangular bounding regions, the convex hull approach is a great improvement.

This system does not use the convex hull approach due to the fact that it was discovered after the system was already using rectangular regions. The rectangular regions work well enough that changing the system to use convex hulls is not currently necessary.