The ``Nothing Inside'' Test

Before the system applies a rule from the grammar, an additional test is made to see if the application of the rule would mean that other nodes end up inside the nodes created as a result of the production.

As long as people do not write formulae with overlapping symbols, this does not restrict the ability of the system to parse mathematical formulae. This approach was independently developed by Miller and Viola  who use the same condition, but testing with convex hulls, to limit the application of rules in their stochastic grammar.

  

Figure 3.12: The ``nothing inside'' test. If a grammar rule collapsed the $\frac {2}{4}$ to a single node, the centre point of the 3 would end up inside its new bounding region. Because of this, the application of the rule is not permitted.

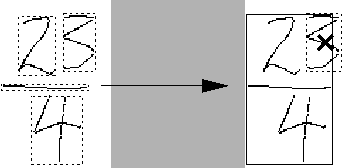
This test is useful because it reduces the number of rules that can be applied in a given situation, but does not limit the ability of the system to parse mathematical formulae. In situations like that shown in Figure , it is possible to apply a fraction rule that collapses the $\frac {2}{4}$ part, leaving the 3 behind. If the $\frac {2}{4}$ were to be collapsed, the 3 would end up inside the new bounding box. Noting this, we can avoid applying the rule.  

  

Figure 3.13: A problem with the no-inside restriction. Collapsing the integral is forbidden due to the fraction bar ending up inside it.

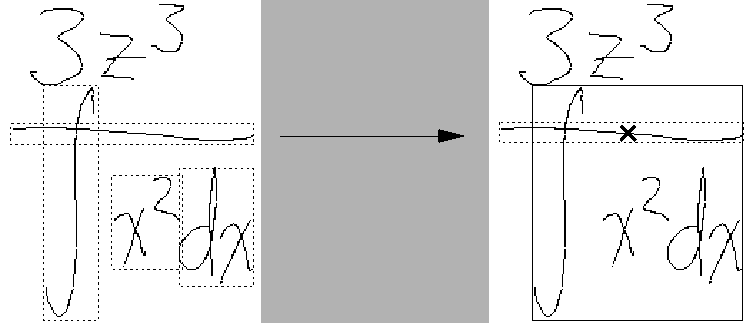A problem arising from the ``nothing inside'' test, is shown in Figure 3.13. A fraction has been written so that the fraction bar overlaps the integral sign. When deciding whether or not to collapse the integral $\int x^2\ dx$, the denominator of the fraction in Figure 3.13, the bounding box that would be created is found to include the centre point of the fraction bar, so the application of the rule is cancelled. This means that the integral will never be collapsed, making the formula unparsable.

Fortunately, as people tend to avoid overlapping symbols as they write, the problem of symbols overlapping each other like this is not common.