Weak Formalisation

The user has to supply fewer boxes in a system using weak formalisation; the grammar now encodes the precedence of operators. The boxes that no longer have to be drawn are those that originally indicated the precedence of operations.

The resulting grammar is called a ``weak grammar'' which uses grammatical categories such as sentence, relation, calculation, term, factor and atom. The priority of operators is encoded using these categories.

For example, to encode the implicit operator precedence of multiplication over function application, for expressions such as ``$\sin xy$'', a grammar can be designed with rules like:
<sin op> $\leftarrow$ $\sin$ <term> and
<term> $\leftarrow$ <term> <factor>

The example formula above is now entered as:

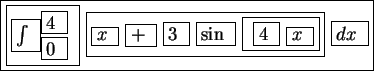
This level of boxing of entries is similar to that used by template based equation editors.