Ambiguity in the Formula

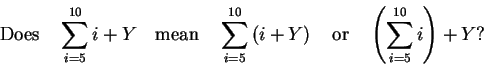
Zhao, Sakurai, Sugiura and Torii  discuss ``tacit agreements'', which fall into two classes: determinable and indeterminable. The indeterminable agreements include the examples of ambiguity that Martin talks about in his paper . One of Martin's examples is:

$$\text{Does}\quad \sum^{10}_{i=5}i+Y \quad\text{mean}\quad \su... ...uad\text{or}\quad \left( \sum^{10}_{i=5}i \right) + Y \text{?}$$

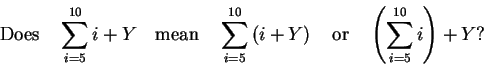
Indeterminable agreements require the knowledge and experience of the reader to resolve. Determinable agreements correspond to rules in the interpretation of formulae, such as the implicit precedence of operations. For example, readers of the formula $a + b \times c$, knowing the standard precedence of mathematical operators, understand that the multiplication operation has precedence over the addition. This means that they interpret it as $a + (b \times c)$ and not $(a + b) \times c$.

Zhao et al. discuss different types of grammars, the complexity of each depending on the level of formality of the formula entry system. More formality means that the user spends more of their time specifying ``boxes'', not dissimilar to the boxes in template-based equation editors, that encode the geometric and logical relationships between various elements in their formulae. The higher the formality, the fewer tacit agreements that have to be encoded into the grammar.

Zhao et al. describe three levels of formalisation: strong, weak, and free. As you move from one to the next the complexity of the grammar increases, as it has to be able to determine more of the tacit agreements in the formulae. Unfortunately, although the strong formalisation is the easiest to write a grammar for, and is the one that offers the most confidence that after processing that you have got the right thing, it also involves the most additional work for the user who is entering formulae. Free formalisation is the exact opposite.

. One of Martin's examples is:

$$\text{Does}\quad \sum^{10}_{i=5}i+Y \quad\text{mean}\quad \su... ...uad\text{or}\quad \left( \sum^{10}_{i=5}i \right) + Y \text{?}$$

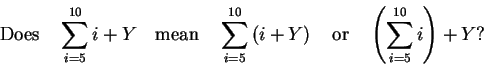
Indeterminable agreements require the knowledge and experience of the reader to resolve. Determinable agreements correspond to rules in the interpretation of formulae, such as the implicit precedence of operations. For example, readers of the formula $a + b \times c$, knowing the standard precedence of mathematical operators, understand that the multiplication operation has precedence over the addition. This means that they interpret it as $a + (b \times c)$ and not $(a + b) \times c$.

Zhao et al. discuss different types of grammars, the complexity of each depending on the level of formality of the formula entry system. More formality means that the user spends more of their time specifying ``boxes'', not dissimilar to the boxes in template-based equation editors, that encode the geometric and logical relationships between various elements in their formulae. The higher the formality, the fewer tacit agreements that have to be encoded into the grammar.

Zhao et al. describe three levels of formalisation: strong, weak, and free. As you move from one to the next the complexity of the grammar increases, as it has to be able to determine more of the tacit agreements in the formulae. Unfortunately, although the strong formalisation is the easiest to write a grammar for, and is the one that offers the most confidence that after processing that you have got the right thing, it also involves the most additional work for the user who is entering formulae. Free formalisation is the exact opposite.