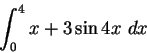
Every structure in a system using strong formalisation has to be put in a box by the user, all determinable and indeterminable tacit agreements are indicated by the user during input. No information is needed in the grammar on the priority of operators, as everything is in a hierarchy of boxes that the user has supplied.
For example, the formula:
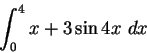
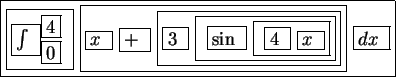
It can be seen that the user has had to explicitly encode the precedence of all the operators, along with specifying the two dimensional layout of the formula, and the arguments for each of the operators.