The Approach Used by This System

Most of the methods considered for segmenting strokes into symbols did not appeal as they either relied on heuristics, or forced the user to have a certain behaviour.

If the character recogniser is able to return confidence information for interpretations of strokes, it is possible to automatically test different combinations of strokes and pick the best. This is a new approach, although is similar to that used by Yaeger, Webb and Lyon  which wasn't seen until afterwards.

The approach that the system uses is to combine overlapping strokes into indivisible units, then use the character recogniser to test groupings of strokes and these indivisible units. This solution works well, only limited by the strength of the underlying character recogniser. While it is less reliable than other stroke segmentation methods, such as the user pausing between characters, it does allow a much more natural and fluid entry of symbols into the system.

The process makes two assumptions: strokes that cross belong to the same character and all the strokes that belong to the one character will be drawn before the user moves onto the next. In other words, all i's must be dotted and all t's crossed before the next symbol is drawn. From casual observation of people writing with pen and paper, and from observation of people using this system, neither of these assumptions interfere with people's writing: most people tend to write like this anyway.

The process used to determine how to segment the strokes supplied by the user works as follows:

• Determine the maximum number of strokes that a symbol can have. This can be determined by analysing the character data set used by the character recogniser. Call this maximum number m.

• Wait until the user has entered 2m strokes, this way there will be at least one fully completed symbol to recognise.

• Collect together all strokes that cross or touch, and call each of these strokes a single ``unit''. For all the remaining strokes, put them all into a unit also, each of these units having one stroke in each. There will be k, 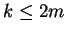$k \leq 2m$ units.

• Generate all possible groupings up the first min(k,m) of these units, and assign a confidence level to each. Each grouping corresponds to a possible grouping of strokes into symbols. The character recogniser is used to recognise the symbols in each grouping and return a confidence level for each symbol. The confidence level for a given group corresponds to the lowest confidence level across the symbols recognised in each group. This technique, of the confidence level of a group as a whole being equal to the lowest confidence within it, is often applied in expert systems .

  Two other methods investigated for determining the confidence of the overall group were:

  • to use a product of the confidences of each symbol within a group. This unfairly penalises groups with more symbols.

  • to use the average confidence of the symbols in a group. Although this worked, it can boost what should intuitively be a low scoring group. For example, if a symbol has a confidence of near zero, other symbols contributing to the average can pull up the overall score.

  The relative confidence scores for two sequences of confidence levels using these three difference methods is illustrated in the following table:

  Symbol Confidences	Minimum	Average	Product
  0.8 0.3 0.1	0.1	0.4	0.024
  0.8 0.3 0.1 0.8	0.1	0.5	0.0192
  0.8 0.0 0.1	0.0	0.3	0.0

• Of all the groups generated, select the group with the highest confidence and return information on the group selected to the user interface. This information includes the stroke groupings and what each group of strokes was recognised as. The system also includes alternative recognitions for each character for use in modify characters mode, described in Section .

With the current character training data, k=4 so all groupings of 1, 2, 3, and 4 units are generated and tested. Due to the assumption that all strokes belonging to the same symbol are drawn in order, we can avoid a combinatorial explosion. The total number of combinations of up to the first k units is 2^k - 1.

  

Figure 4.4: All groupings for four units.

Figure 4.4 illustrates the new method developed for generating all the groupings of up to four units. To generate all groupings of n units, the tree is built starting with a parent node of n 1's. The children of a node are then created by the addition of all adjacent pairs of boxes. Children that already exist elsewhere in the graph are not generated. The children that are not generated are represented by dotted boxes.

These groups indicate the groupings of strokes to try. For example, the group ``1 2 1'' means: ``Take the first unit on its own, then the next two units together, then the last unit on its own.''