 |
Excessively sloped formulae can be difficult to process reliably, no matter how good the underlying formula processor is. This is because the geometric relationships become ambiguous.
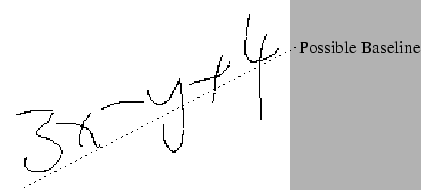
Figure 3.14 shows a skewed formula. While the author perhaps intended it to be 3x-y+4, it is most likely to be parsed as 3x-y+4.
In sloped formulae, the positions of the symbols are most commonly skewed, but the symbols themselves are not rotated. A brief investigation into the automatic straightening of formulae was carried out. Least squares linear regression and Hough transforms were used to attempt to determine the baseline of symbols entered. From the baseline determined, formulae were then skewed to bring the baseline back to horizontal. While it was occasionally helpful and showed initial promise, it had trouble with short formulae, and formulae with exponentials or subscripts. For example, if the formula shown in Figure 3.14 was meant to be 3x-y+4, the slope correction would ``correct'' it to 3x-y+4.
These ambiguities can be difficult to resolve in general, but attributes such as the relative size of symbols can be used. For example: knowing that exponents are typically smaller than the base symbol, top-right arcs will be only be built if the target node is smaller than the parent node. Care has to be taken, however, if the target node is a subexpression in a formula.