 |
Arcs are not built between two nodes if any other bounding regions, belonging to other symbols or subexpressions, are crossed by a line running between the centre points of the symbols or subexpressions being linked. Within the subset of mathematical formulae this system can currently process and to the limit of my mathematical knowledge, this will not restrict the system in any way.
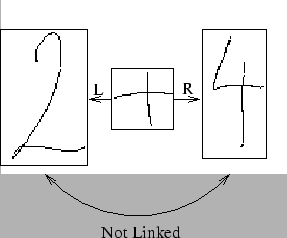
Figure 3.11 shows a situation where an arc is not built. There is no link built between the 2 and the 4 because the +'s bounding box is on the line between the centres of the 2 and 4.
This process for building the graph works well, though possibly building too many arcs in the graph due to too much leniency in the geometric test. Unfortunately, this is a trade off between having too many arcs but being able to parse sloppy formula, and between having a more modest number of links, but requiring the input to be neat and closely spaced.
The complexity of building all the arcs in the graph varies between O(n2) and O(n3), where n is the number of nodes in the graph. The variability is due to the fact that, if the initial O(1) type and geometric tests fail, then the arc building algorithm can rule out having to carry out the O(n) overlap test.
Continuing the earlier example, Figure 3.6(b) shows the initial graph for the formula with the arcs built. Note, for example, that there is no link between the ``x'' and ``4''. Although the 4 is a subscript position relative to the x, no link is built because it would pass over the fraction bar.