Ambiguous Symbols

Some symbols have many possible meanings and a distinction can only be made by examining it in the context of surrounding symbols. Examples of unambiguous symbols, and several ambiguous ones are listed here.

• ``!'' is always a postfix factorial operator. Its argument can always be found to its immediate left.

• ``$\int$'' is always an integration operator, but we do not know how many arguments it has. There will be an integrand and a differential (the ``dx'' part), but either zero, one or two limits.

• ``-'' (a horizontal line) can be an infix subtraction operator, a prefix negation operator, or a fraction bar. It is also possible that it is part of some other symbol, such as =, $\leq$, or $\subseteq$.

• ``.'' (a dot) can be multiplication, a decimal point, part of a symbol, or an annotation, e.g.: 3x.y, 2.71828, !, or $\dot{x}$.

• a_ij can mean either the array element a(i,j): the ith row in the jth column in a 2D array, or $a(i \times j)$: the element which is the product of i and j in a 1D array.

• The a in ``X^a'' can either be a power or, as some authors use it, an index into an array.

Some of the ambiguities listed above are concerned with understanding the underlying meaning of things: their semantics. Others are to do with syntax. For example, the last case is to do with semantics. Determining the meaning of X^a is impossible without the knowledge of what the author intended it to mean. The second example above, determining the number of limits on an integral, is a syntactical problem. If a limit is found, its function is unambiguous. The problem is that the number of limits to look for is indeterminable in advance.

A large amount of reliance is placed on the knowledge and experience of the person reading mathematical formulae. They are expected to understand the context in which something is written, and thus interpret things correctly. To build such experience into an automated system can be difficult.

If the purpose of parsing the formula is to produce L^ATEX that generates output that looks like the user's input, determining the underlying meaning is not as important; we are only interested in appearance, not meaning. If we are generating input for mathematical computation packages, such as Mathematica or Matlab, to do calculations with or operations on the formulae, then it is important to know the underlying meaning of conventions that the formula's author uses, so that a correct command string can be produced.

Anderson  and Bernstein  believe that syntax and semantics of a formula are different, and say that the parsing stage should only return something which describes the layout of the formula. Bernstein's view is that if we are intending to pass the formula onto some later stage that has its own input format, then the problem of going from the layout description to this input format should be done as a subsequent stage of processing. This could be done, for example, with a 1D string parser.

 

An example of a formula represented by a layout description follows. This is taken from the paper by Fateman, Tokuyasu, Berman and Mitchell .

The formula

$$\int{\frac{x^q-1}{x^p-x^{-p}}\frac{dx}{x}}= \frac{\pi}{2p}\tan\frac{q\pi}{2p}$$

is represented in a positional notation as:

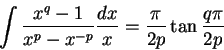
(hbox
  (vbox integral nil nil)
  (vbox quotient
        (hbox (expbox x q) - 1)
        (hbox (expbox x p) -
        (expbox x (box - p))))
  (vbox quotient
        (hbox d x)
        x)
  =
  (vbox quotient
        pi
        (hbox 2 p))
  Tan
  (vbox quotient
        (hbox q pi)
        (hbox 2 p)))

The hbox and vbox are operators that perform horizontal and vertical concatenation of symbols and subexpressions, in a similar manner to the concatenation operators that Martin uses , described in Section . For example, a fraction is a vertical concatenation of the numerator, a horizontal line and the denominator.

Splitting the formula processor into two parts with the first stage being a layout processor returning a description of the layout of the formulae, and the second stage being a formula processor that takes the layout description and returns the command-string for the formula, has the advantages that:

• it breaks the system into two distinct, independent, simpler stages.

• the layout processor does not have to take into account the meaning of the formula, as it is not the final stage in the process. As a result it decouples the layout processor from the formula processor, simplifying its code. All author-dependent customisation can be done at the level of the formula processor, independent of the layout processor.

• either the layout processor or formula processing unit can then be easily taken out and replaced with minimal effort. Each unit in itself is relatively simple with respect to a combined function unit, and has very well defined inputs and outputs.

It can also be argued that a single combined function unit can provide the same thing, if it uses a carefully chosen final language. For example, LISP-like notation essentially describes the layout of a formula. Splitting the process into two parts means you have to write a parser that will take the positional description and output a more human-readable version, such as L^ATEX or a Mathematica command string. It also makes it harder for the layout processor to use contextual information in making choices in ambiguous situations, as the layout processor is now a separate part.