Negative

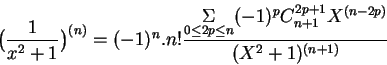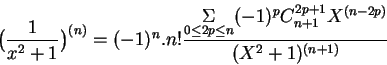
There were only two major problems with the system found by participants in the user testing. First was the implementation of the graph rewriting parser, its lack of speed and errors when processing formulae. Second were the incidental problems related to the character recogniser not being trained for each user's writing, which resulted in high misgrouping and misrecognition rates.

Both of these problems can be addressed; the first through improvement of the graph rewriting parser, the second through either improving the character recognition module, or transparently training the character recogniser online using the corrections that the user supplies through the modify character mode. Other problems found with the user interface were minor in nature and typically cosmetic.

The system is going to need to be able to handle more complex formulae before it will be of use to a mathematician. For example, a formula such as one that Lavirotte and Pottier's system  can parse:

$$\big(\frac{1}{x^2+1}\big)^{(n)} = (-1)^n.n!\frac{\underset{0\... ...q n}{\Sigma} (-1)^pC^{2p+1}_{n+1}X^{(n-2p)} }{(X^2+1)^{(n+1)}}$$

is unable to be handled by this system, due to the time required by the parser being excessive. Thus, improving the parser to take advantage of contextual information and to use optimised graph searching techniques is important, if further work is to be done on this system.

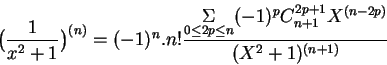
can parse:

$$\big(\frac{1}{x^2+1}\big)^{(n)} = (-1)^n.n!\frac{\underset{0\... ...q n}{\Sigma} (-1)^pC^{2p+1}_{n+1}X^{(n-2p)} }{(X^2+1)^{(n+1)}}$$

is unable to be handled by this system, due to the time required by the parser being excessive. Thus, improving the parser to take advantage of contextual information and to use optimised graph searching techniques is important, if further work is to be done on this system.