Geometric Test

A geometric check is made to ensure that the symbols or subexpressions that nodes represent are actually arranged the way that an arc between these nodes implies they are.

  

Figure 3.7: Regions used by the geometric check.

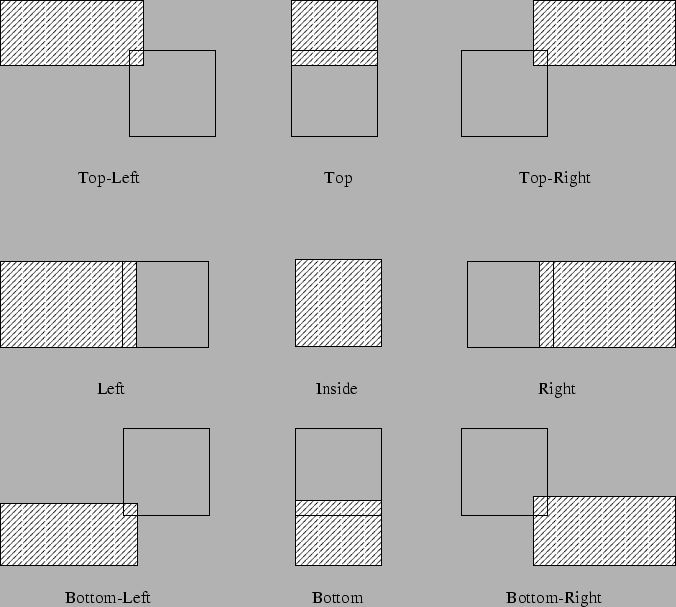
Figure 3.7 shows the regions used by the geometric check. There are nine regions, including an ``inside'' region, all defined relative to the first symbol's bounding box. Note that neighbouring regions, for example the ``top-right'' and ``right'' regions, overlap. This helps deal with problems occurring when people accidentally write characters too close to one another and end up with overlapping bounding boxes. It also allows some leniency in the placement of characters.

  

Figure 3.8: Is ``A'' to the top-right of ``B''? Yes.

Before building an arc between two nodes A and B that would encode relationship x, it is tested to see whether or not symbol A is actually geometrically x of B. The centre point of A's bounding box is tested against the regions defined in terms of the dimensions of B's bounding box. Figure 3.8 illustrates the check to see if A is to the top-right of B. This approach of using rectangular regions is also used by Littin .

Symbols have to be sufficiently close to one another to be linked. The impact of this on the user is that symbols in their formulae cannot be spread out too much. Increasing the maximum range means that the user can space things out more, but the graph builder ends up putting more false connections between nodes, which then results in longer and more erroneous parsing.

There are a variety of ways of dividing up the input area around each character to determine which areas are ``to the right'' and ``above'', etc. An alternative approach to the rectangular subdivision of the input area is to test based on the angle that the line between the centre points of the items concerned makes with horizontal. For example, an item is to the ``right'' of another if the angle is between $-22.5^\circ$ and $22.5^\circ$.

  

Figure 3.9: As the length of the exponent grows, it moves from the ``top-right'' to the ``right'' region.

(a)

(b)

This works well for individual symbols, but fails for groups of symbols such as subexpressions in a formula. Figure  illustrates this. In Figure 3.9(a) B is in the ``top-right'' region relative to A. However, if the length of the superscript B grows, as in Figure 3.9(b), its centre point moves into the ``right'' region. Using a rectangular subdivision, as this system does, or other shaped regions, such as that used by Lavirotte and Pottier  avoids this problem.

  

Figure 3.10: The shape of the ``right'' region that Lavirotte and Pottier use.

Figure  shows the region Lavirotte and Pottier use for ``right''. The shape of this region is based on the fact that most mathematical notations, while 2D, are based on normal reading, from left to right. As a result, symbols which have a ``top-'' or ``bottom-'' aspect to them are typically close to the parent symbol, while horizontal links (such as ``left'' and ``right'') can be far off. This is a good idea as it means that fewer erroneous links will be built. The idea behind this technique has been used by this system by making the height of the geometric regions involving a ``top'' or ``bottom'' component less than that for ``left'' and ``right''.