Background

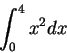
Mathematical formulae have a two-dimensional nature. A lot of information is conveyed through the relative positions of symbols in a formula: the operation that is being applied to the symbols, or what the arguments to a function are. Original systems for doing mathematics on a computer were developed in the times of character-only interfaces . As a result, formulae were entered as a linear text string of ``commands''. Graphical entry was out of the question as the equipment required was either unavailable, or prohibitively expensive.

A linear command string can represent all the same formulae as a traditional two-dimensional notation. Turning a two-dimensional formula into a linear representation does not incur a loss of information, but it is necessary to know the overall structure before it can be linearised. In effect, the user has to do a mental ``parse'' of the formula to determine its structure before starting to enter it.

Even with the proliferation of graphic capable displays and pointing devices such as mice or pens and tablets, applications and systems are still produced with the option of, or even restricted to, the use of keyboard entry for formulae.

Entering a formula as a command string is not very difficult if you have the formula in front of you and are just transcribing it, assuming you have a knowledge of the command language you are using. It is only when you are trying to write a formula from a ``mental image'', or want to manipulate it afterwards, that it becomes difficult.

 For example, L^ATEX  is a non-WYSIWYG system for creating and typesetting documents, using text commands for all layout and description of the structure of a document. The entry of formulae is also through a command language. The formula:

$$\int^{4}_{0}{x^2}dx$$

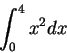
is entered into L^ATEX as \int^{4}_{0}{x^2}dx. While this is not complex, the structure of a formula becomes a lot harder to visualise and manipulate as the length of its command string grows. For example, the formula:

$$f(a) = \frac{1}{2\pi i} \int^{2\pi}_{0}{ \frac{f(e^{i\theta})... ...e^{i\theta})} \frac{d}{d\theta} (T^{-1}(e^{i\theta})) d\theta}$$

is entered as:

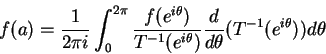
f(a) = \frac{1}{2\pi i} \int^{2\pi}_{0}{
\frac{f(e^{i\theta})}{T^{-1}(e^{i\theta})} \frac{d}{d\theta}
(T^{-1}(e^{i\theta})) d\theta}

By looking at the command string for this formula, it is difficult to gain an idea of its overall structure. Furthermore, changing the layout of the components in the formula, or performing other major editing operations is very difficult.

The people who are most likely to benefit from the ability to carry out mathematics on a computer are also the ones who are least likely to be interested in typing in complex or unnatural notations for formulae. Mathematicians would have spent many years of their lives using pencil and paper, a method which does allow 2D input and display. In spite of the enormous potential offered by computers for mathematical computation and manipulation, a simple means of entry still does not exist.

While most computer algebra systems have graphical formula entry front-ends available, for example Mathematica , sometimes this front-end is unavailable for the particular package of interest, or difficult to use. Typically these are template based editors, where the user chooses a template for the operation they desire, and fills in the boxes provided by the user interface. While template systems are a step towards the goal of being able to enter formulae while keeping their two dimensional layout, they are still not as fluid to use as a pencil and paper and still require a mental pre-parse of formulae to determine their structure before entry.

An ideal computer-based mathematics system would be one that had the ease of use of pencil and paper but with the power of a computer behind it. A user would be able to enter their formula as they would write it on a piece of paper: drawing with a pen on a tablet and having their strokes appear on the screen. Once the user had drawn their formula, they would then be able to freely manipulate, add to and change the formula as they desired. Once the formula was entered to their satisfaction, the system could then insert it into their word processor, L^ATEX document, or other application. Should the formula entry system be part of a WYSIWYG system, a typeset version of the formula could be displayed. If it was part of a computer algebra system, they could evaluate or perform other operations such as expansion, simplification, or evaluation of it.

This thesis describes a new system that is a step towards the ideal system described above: the Freehand Formula Entry System (FFES). It allows the freehand entry and editing of formulae using a pen and tablet. Automatic handwritten formula recognition is then used to generate a L^ATEX command string for the formula.

The system consists of a number of independent modules:

• A handwriting recogniser that recognises the strokes input by the user to determine the symbols written.

• A formula processor which takes the list of symbols and their positions, and returns the formula they represent.

• A user interface which provides transparent interaction with the handwriting recogniser and formula processor. The user interface provides easy entering and manipulation of formulae, along with the means to correct any errors made by the other components in the system.

The handwriting recognition module was developed as part of a larger system , and the formula processor is an implementation of published techniques . The synthesis and evaluation of these modules and the user interface are the main contribution of this thesis. The user interface includes a new method for automatically determining the correct grouping of the user's strokes into symbols and a number of new user interface tools. The tools enable the user to easily correct the inevitable mistakes made by the character recogniser and automatic stroke grouping process.

This thesis also reports on user testing carried out on this system. It was found that a pen-based formula entry system is easier and more comfortable to use over existing formula entry systems, both for the initial entry and subsequent editing of formulae.

Chapter  reviews existing formula processors and formula entry systems. Each formula processor is analysed and its suitability for handwritten formula interpretation is discussed. Chapter 3 describes in detail the implementation of the formula processor, a subset of the system described by Lavirotte and Pottier .

Chapter  describes the new user interface designed and implemented for the freehand entry and editing of formulae, including the new techniques developed for automatically grouping a user's strokes, and correcting errors that arise as the user enters their formula.

Chapter 5 describes user testing and how the user testing of this system was conducted. Chapter 5 also discusses usability inspections. Chapter 6 is an evaluation of the system, based on results of the user testing and an informal usability study. Chapter 7 discusses directions that further development of the system could take, in response to issues and ideas raised in Chapter 6.

The final chapter, Chapter 8, summarises the findings and contributions of this thesis, and suggests some future avenues of research.